MIPLearn/docs/problems.md

Benchmark Problems, Challenges and Results

MIPLearn provides a selection of benchmark problems and random instance generators, covering applications from different fields, that can be used to evaluate new learning-enhanced MIP techniques in a measurable and reproducible way. In this page, we describe these problems, the included instance generators, and we present some benchmark results for LearningSolver with default parameters.

Preliminaries

Benchmark challenges

When evaluating the performance of a conventional MIP solver, benchmark sets, such as MIPLIB and TSPLIB, are typically used. The performance of newly proposed solvers or solution techniques are typically measured as the average (or total) running time the solver takes to solve the entire benchmark set. For Learning-Enhanced MIP solvers, it is also necessary to specify what instances should the solver be trained on (the training instances) before solving the actual set of instances we are interested in (the test instances). If the training instances are very similar to the test instances, we would expect a Learning-Enhanced Solver to present stronger perfomance benefits.

In MIPLearn, each optimization problem comes with a set of benchmark challenges, which specify how should the training and test instances be generated. The first challenges are typically easier, in the sense that training and test instances are very similar. Later challenges gradually make the sets more distinct, and therefore harder to learn from.

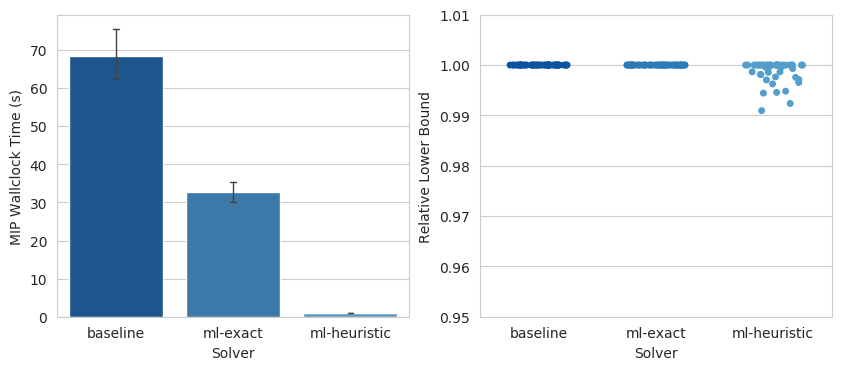
Baseline results

To illustrate the performance of LearningSolver, and to set a baseline for newly proposed techniques, we present in this page, for each benchmark challenge, a small set of computational results measuring the solution speed of the solver and the solution quality with default parameters. For more detailed computational studies, see references. We compare three solvers:

• baseline: Gurobi 9.0 with default settings (a conventional state-of-the-art MIP solver)
• ml-exact: LearningSolver with default settings, using Gurobi 9.0 as internal MIP solver
• ml-heuristic: Same as above, but with mode="heuristic"

All experiments presented here were performed on a Linux server (Ubuntu Linux 18.04 LTS) with Intel Xeon Gold 6230s (2 processors, 40 cores, 80 threads) and 256 GB RAM (DDR4, 2933 MHz). All solvers were restricted to use 4 threads, with no time limits, and 10 instances were solved simultaneously at a time.

Maximum Weight Stable Set Problem

Problem definition

Given a simple undirected graph G=(V,E) and weights w \in \mathbb{R}^V, the problem is to find a stable set S \subseteq V that maximizes \sum_{v \in V} w_v. We recall that a subset S \subseteq V is a stable set if no two vertices of S are adjacent. This is one of Karp's 21 NP-complete problems.

Random instance generators

The class MaxWeightStableSetGenerator can be used to generate random instances of this problem, with user-specified probability distributions. When the constructor parameter fix_graph=True is provided, one random Erdős-Rényi graph G_{n,p} is generated during the constructor, where n and p are sampled from user-provided probability distributions n and p. To generate each instance, the generator independently samples each w_v from the user-provided probability distribution w. When fix_graph=False, a new random graph is generated for each instance, while the remaining parameters are sampled in the same way.

Benchmark challenges

Challenge A

• Fixed random Erdős-Rényi graph G_{n,p} with n=200 and p=5\%
• Random vertex weights w_v \sim U(100, 150)
• 300 training instances, 50 test instances

MaxWeightStableSetGenerator(w=uniform(loc=100., scale=50.),
                            n=randint(low=200, high=201),
                            density=uniform(loc=0.05, scale=0.0),
                            fix_graph=True)

Benchmark results

Challenge A